自组织神经网络，又称为自组织竞争神经网络,特别适合于解决模式分类和识别方面的应用问题。这类网络采用无监督机器学习算法，利用训练数据集的内在规律对样本空间进行降维和离散化表示(map)。不同于其他人工神经网络，自组织网络使用邻域函数(neighborhood function)来保留原始输入空间的位置信息。本文终点讨论用途最广泛的 Self-Organizing Map (SOM)。

SOM的概念来源于大脑神经在处理信息时，处理相似信息的神经元往往距离很近，会组成一个个区域（见下图）。一般来说，SOM的隐藏层分布在一个二维平面中，通过计算样本实例与输入-隐藏层之间的weight vector的距离，来找到距离样本最近的隐藏层神经元，继而通过二维平面上的坐标，将高维样本转化为二维样本。值得注意的是，降维后的二维数组仍然保持了原高维空间中的距离性质，因此在原空间中距离相近的样本点在二维空间中距离依然相近。现有的研究已经表明，拥有少量节点的SOM的聚类表现与k-means类似，而大量节点构成的SOM可以刻画出数据分布的本质特性。在降维方面，SOM看作是PCA的非线性扩展，在降维效果上不会比PCA差。

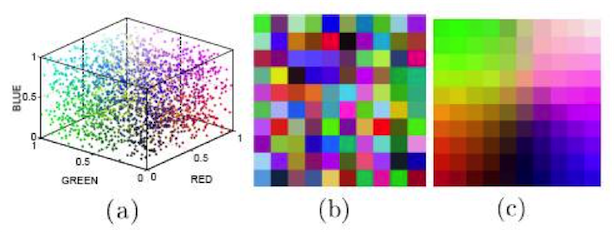
下图是SOM对色彩进行聚类的可视化结果。由于颜色由RGB三色构成，在三维空间的分布如下图(a)所示。图(b)是初始化权重的可视化结果，图(c)是SOM算法运行收敛后的权重可视化，可以发现隐藏层中网络距离(2维)接近的神经元会有相似的连接权重(3维)。

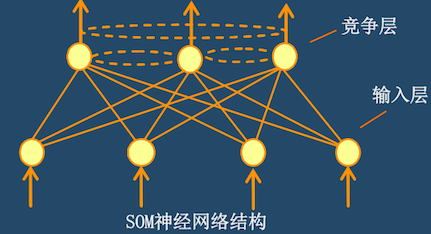
SOM网络结构

基本上为输入层和隐藏层（竞争层）的双层结构,隐藏层的邻接神经元互相连接。如下图所示。

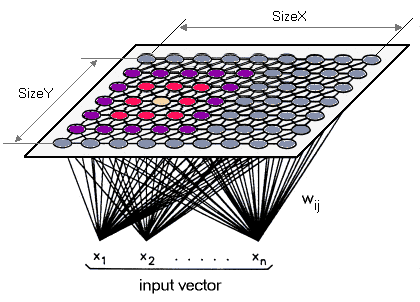
一般而言，SOM的隐藏层是一个二维平面，下图展示了立体空间中的一种SOM隐藏层连接结构(square grid)。每个输入神经元到所有的隐藏层神经元都有连接。例如，输入层共$n$个神经元，隐藏层共$X \cdot Y$个神经元，那么从输入层到隐藏层的连接总数为$n \cdot X \cdot Y$。而隐藏层神经元之间的连边并无消息的传递，只是提供了一个网络的拓扑结构以方便计算神经元之间的距离。

SOM算法流程

(1) 网络初始化

• 用随机数设定输入层和隐藏层之间权值的初始值

(2) 输入向量

• 把输入向量传递给输入层

(3) 计算隐藏层的权值向量和输入向量的距离

• 隐藏层的神经元$j$和输入向量 $\vec{x} \in R^n$ 的距离可以根据具体的task指定，这里采用欧式距离： $$d_j = \sqrt{ \sum _{i=1}^n (x_i - w_{ij})^2 }$$

(4) 选择与权值向量的距离最小的神经元

• 计算并选择使输入向量和权值向量的距离最短的神经元，把其称为胜出神经元并记为 $j^ *$，并给出其邻接神经元集合$j \in nbr(j^*)$。

(5) 调整权值

• 胜出神经元和位于其邻接神经元的权值按下式更新： $$w_{ij}(t+1) = w_{ij}(t) + \alpha \cdot h(j,j^*) \cdot (x_i - w_{ij})$$

其中，$\alpha$是学习速率，$h(j,j^*)$是关于神经元$j$与$j^*$的邻域函数。一般选择高斯函数作为邻域函数：$h(j,j^*) = exp \left( - \frac {(j-j^*)^2}{\sigma ^2} \right)$ 。

(6) 判断是否达到预先设定的要求。如达到要求则算法结束，否则返回(2)，进入下一轮学习

SOM算法细节

• 神经元的权重初始化方法主要有两种：随机数和PCA空间随机采样。后者在训练数据的前两个主成分维度张成的空间中随机采样构成初始权重（$w = \alpha \cdot \lambda_1 + \beta \cdot \lambda_2$）。而后者可以提高SOM的训练收敛速度，因为一般来说初始权重已经近似表示了数据的主要分布特征。（我认为，当特征中的随机误差较大时，可以在ICA空间中采样）

• 由邻域函数可以看出，以胜出神经元为中心设定了一个邻域半径，称为胜出邻域。学习初期，胜出神经元和其附近的神经元全部接近当时的输入向量，形成粗略的映射。$\sigma$ 随着学习的进行而减小，胜出邻域变窄，胜出神经元附近的神经元数变少。因此，SOM学习方法是一种从粗调整向微调整变化，最终达到预定目标的过程。

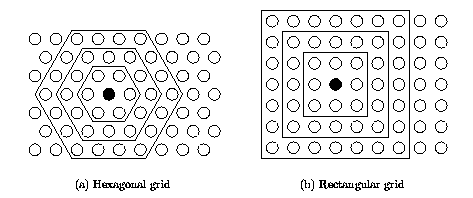
• 样本间距离的度量对与降维和聚类至关重要，本文中选择的是欧式距离进行度量，然而在实际问题中，欧氏距离不见得最好，因而有必要设计一个良好的距离度量，甚至采用metric learning来学习距离度量。

SOM算法实例

为了简单说明算法计算流程，在一个包含有3个输入神经元和2个隐藏层神经元的SOM上训练2例样本：[0.8 0.7 0.4], [0.6 0.9 0.9]。初始权重和网络结构如下图所示。领域半径为0，学习率为0.5。在训练时按顺序给SOM输入样本，每输入一个样本调整一次权重。

输入向量1到隐藏层神经元权重的欧氏距离分别是：

$$d_1 = (0.5-0.8)^2 + (0.6-0.7)^2 + (0.8-0.4)^2 = 0.26$$ $$d_2 = (0.4-0.8)^2 + (0.2-0.7)^2 + (0.5-0.4)^2 = 0.42$$ 输入向量距离隐藏层神经元1的距离更近，因此更新隐藏层神经元1的权重（如果领域半径非0，则还要更新领域内所有神经元的权重）： 根据 $$w_{ij}(t+1) = w_{ij}(t) + \alpha \cdot h(j,j^*) \cdot (x_i - w_{ij})$$ 有： $$w_{11} = 0.65 = 0.5 + 0.5(0.8 - 0.5)$$ $$w_{12} = 0.65 - 0.6 + 0.5(0.7 - 0.6)$$ $$w_{13} = 0.6 = 0.8 + 0.5(0.4 - 0.8)$$

输入向量2到隐藏层神经元权重的欧式距离分别是：

$$d_1 = (0.65-0.6)^2 + (0.65-0.9)^2 + (0.6-0.9)^2 = 0.155$$ $$d_2 = (0.4-0.6)^2 + (0.2-0.9)^2 + (0.5-0.9)^2 = 0.69$$ 输入向量距离隐藏层神经元1的距离更近，因此更新隐藏层神经元1的权重（如果领域半径非0，则还要更新领域内所有神经元的权重）： 根据 $$w_{ij}(t+1) = w_{ij}(t) + \alpha \cdot h(j,j^*) \cdot (x_i - w_{ij})$$ 有： $$w_{11} = 0.625 = 0.65 + 0.5(0.6 - 0.65)$$ $$w_{12} = 0.775 - 0.65 + 0.5(0.9 - 0.65)$$ $$w_{13} = 0.750 = 0.60 + 0.5(0.9 - 0.6)$$

参考文献

[1] https://en.wikipedia.org/wiki/Self-organizing_map

[2] http://alaric-research.blogspot.com/2011/02/self-organizing-map.html

[3] T. Kohonen, “The Self-organizing map,” Proceedings of the IEEE, Vol. 78, No. 9, pp.1464-1480, Sep. 1990.

[4] F. Jiang, H. Berry, and M. Schoenauer, The impact of network topology on self-organizing maps, Proceedings of the first ACM/SIGEVO Summit on Genetic and Evolutionary Computation, pp.247–254, 2009.